难度:★★★★☆(涉及到认识一个全新的坐标系)
兴趣:★★★★☆(运动的时空到底发生了什么变化?这也是理解时空扭曲的基础)
阅读提示:请大家与我一起,顺着文本的逻辑,理解加粗的概念。【斜体字】为补充的概念或者更加详细的解释说明,可以选择性地阅读。
一、光速不变
上一期得到的两个更像哲学观点的结论——“运动的相对性”与“时空的等价性”,还不足以得到爱因斯坦的狭义相对论。
二十世纪初,随着科学实验的推进,“光速不变”的假设被提出并且证实。即,在任何参考系中看同一束光,它的速度始终为300000km/s。这样的发现直接颠覆了经典的时空观,促使了洛伦兹变换与狭义相对论的发现。
对于一般“快速”的物体,例如跑车,它相对于地面的速度可以达到200km/h,但是在10km/h追逐它的人的眼里,它的速度将是190km/h。但光则不一样,不论以多快的速度追逐,它的速度始终是300000km/s。这样的规律产生了许多有趣的结果,虽然这些结果都因为光速实在是太快,而十分微弱。
相对运动的参考系里,空间拥有了不一样的“比例尺”,相对运动的物体,在运动方向上会更短!物体本身的长度并没有变,只是在地面参考系上看,物体参考系里的“一米”更短了。这甚至有物理瘦身的功效,只要能达到飞机速度的二十万倍就能瘦1%呢!

在相对运动的参考系里,时间的“比例尺”也不同。如果一架以非常快的速度远离(或接近)地球的宇宙飞船,那里的时间的流逝速度将比地球慢。也许在飞船返回时,飞船里的哥哥就会变成弟弟!
二、把时空……画出来!
在前两个例子中,时间和空间分别都出现了拉伸与收缩,但是这并不是时空扭曲。请允许我慢慢道来:
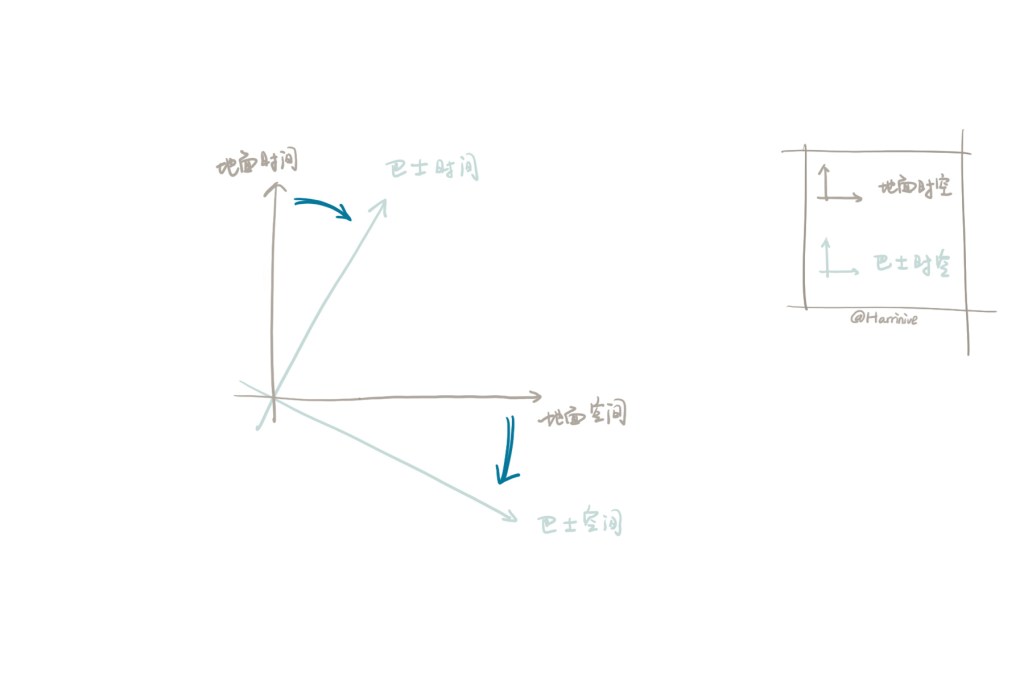
为了用图片表示一个时空,我们绘制这样的坐标轴(参考系),横坐标是空间上的位置信息,纵坐标是时间上的时刻信息。这张平面图上,每一个点都代表一个事件,在特定位置与特定时刻发生,许多事件点会组成事物在时空中移动的轨迹。例如,下面这张图展示了地面参考系,横坐标代表了一条延伸的公路。人和车都沿着公路移动,每一条线都代表了人或车在时空中的移动轨迹。
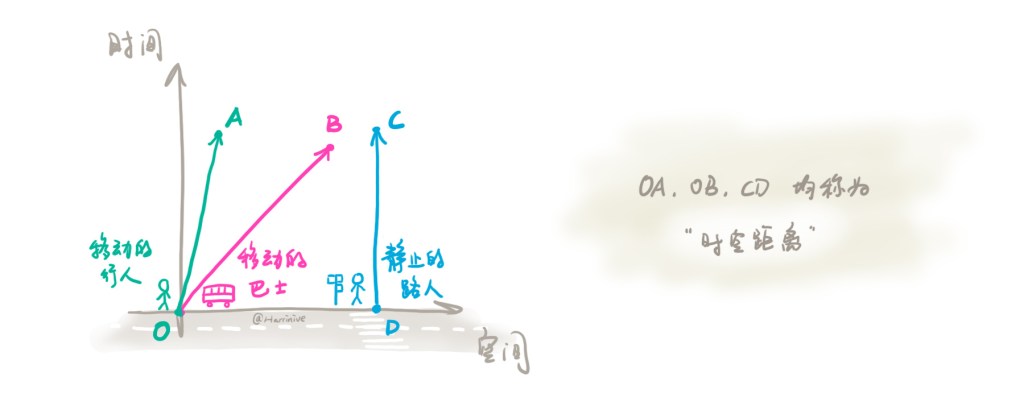
在这样的图里,任意两个点之间的直线段的长度,叫做“时空距离”。在图里,OA、OB、DC的长度均称为时空距离。【事实上,这个定义是错误的,在这里这样定义“时空距离”,仅为了定性地介绍原理。时空距离实际上是:dx^2 – dt^2。】
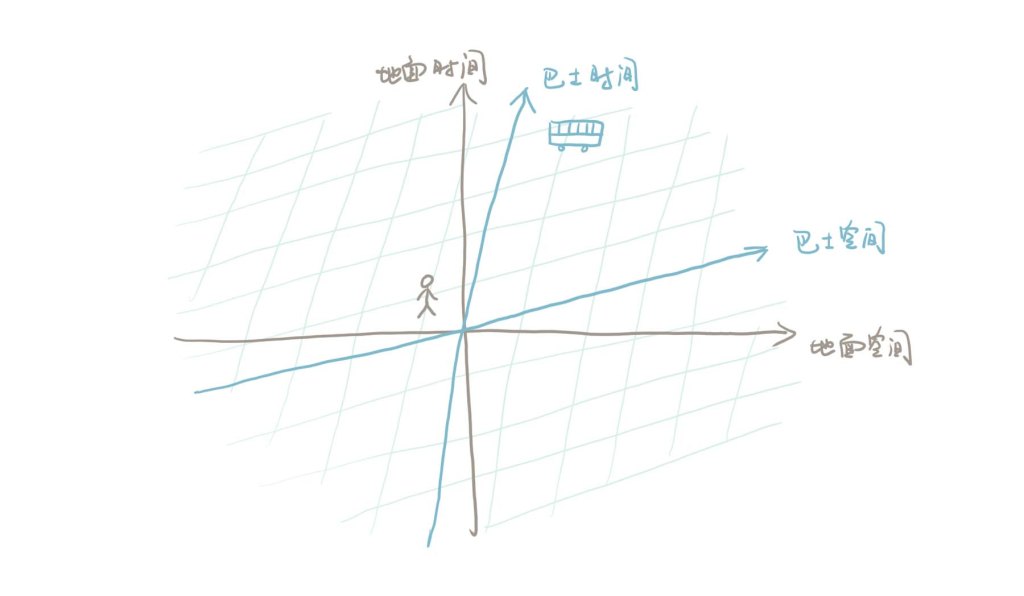
上面的图只展示了地面参考系,那么该如何绘制巴士参考系呢?由于在巴士里,乘客是相对静止的,他们只感受到时间的流逝,而没有位置的移动,那么我们可以这样画巴士里的时空(浅蓝色参考系):
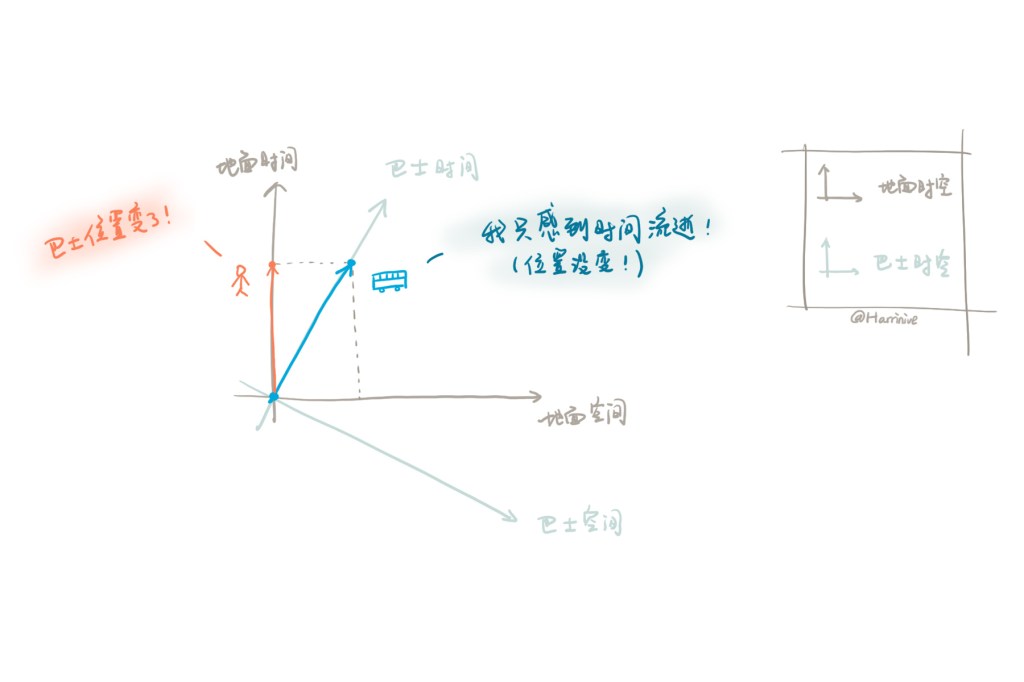
图里清楚的展示了,在地面上,路人会观察到巴士上的时刻和位置不断变化。而在巴士时空里,巴士并没有空间位置的移动。
【我需要再次强调这个图是有误的,因此我们只能定性的寻找可能出现的现象,而不能定量地观察大小区别】我们还能发现一些现象,例如巴士经历的时间(蓝线长度)和地面上观察到它经历的时间(黄线长度)不同。
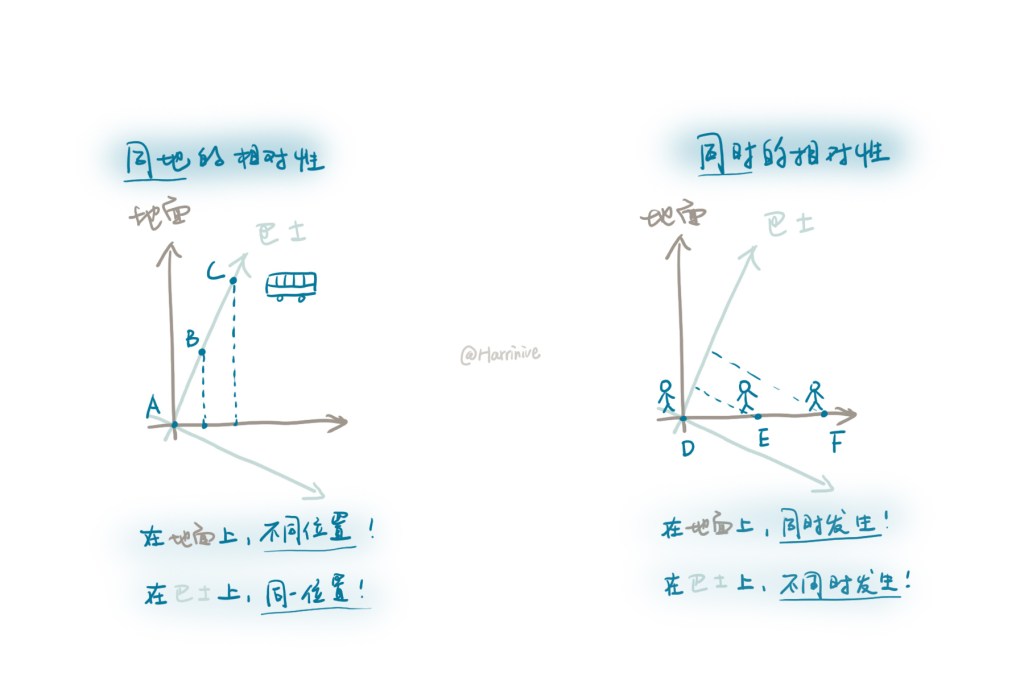
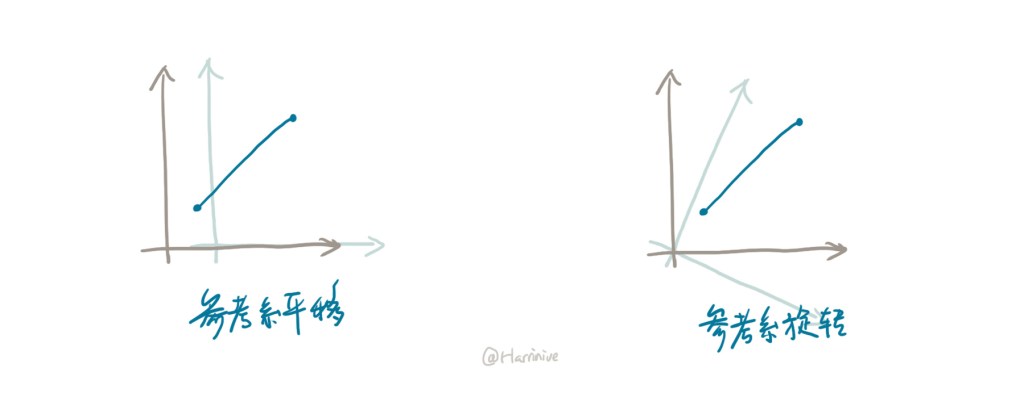
不仅如此,同地的相对性与同时的相对性也在图里完美的体现出来。下方左图描述了同地的相对性:在地面上看(棕色参考系),巴士在不同时间(纵坐标)出现在了不同位置(横坐标);而在巴士上看(浅蓝色参考系),巴士在不同时间出现在了同一位置。而下方右图则体现了同时的相对性:在地面上看,不同位置的事件同时发生(纵坐标不同);而在巴士上看,这些事件不同时发生。
三、时空旋转
我们发现,时空确实没有扭曲,而是旋转了!!狭义相对论表明,和我们相对匀速运动的时空只与我们的时空相差一个参考系的旋转。
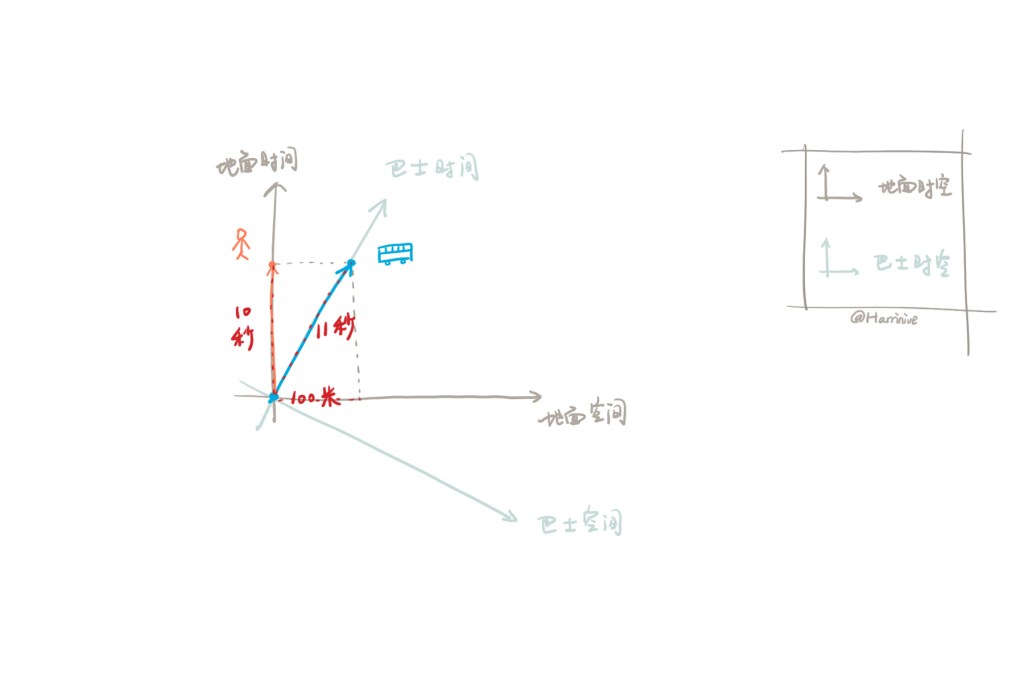
旋转一个参考系,将会改变事件的空间位置和时刻(时空坐标)。在地面参考系中,巴士在10秒内,前进了100米;而在巴士参考系中,它却经历了11秒,且没有运动。【实际上巴士经历的时间比10秒短,且与10秒差别极小】
但是旋转参考系,不改变时空距离。旋转变换与平移变换都不改变原本的时空距离,这是经典几何原理的展示,也是光速不变原理的重要推论。一个苹果旋转、平移以后还是苹果,维持原样,时空也是如此。此外,由于在巴士参考系中,时空距离就是巴士所经历的时间,这段长度被更普遍地称为“固有时”。
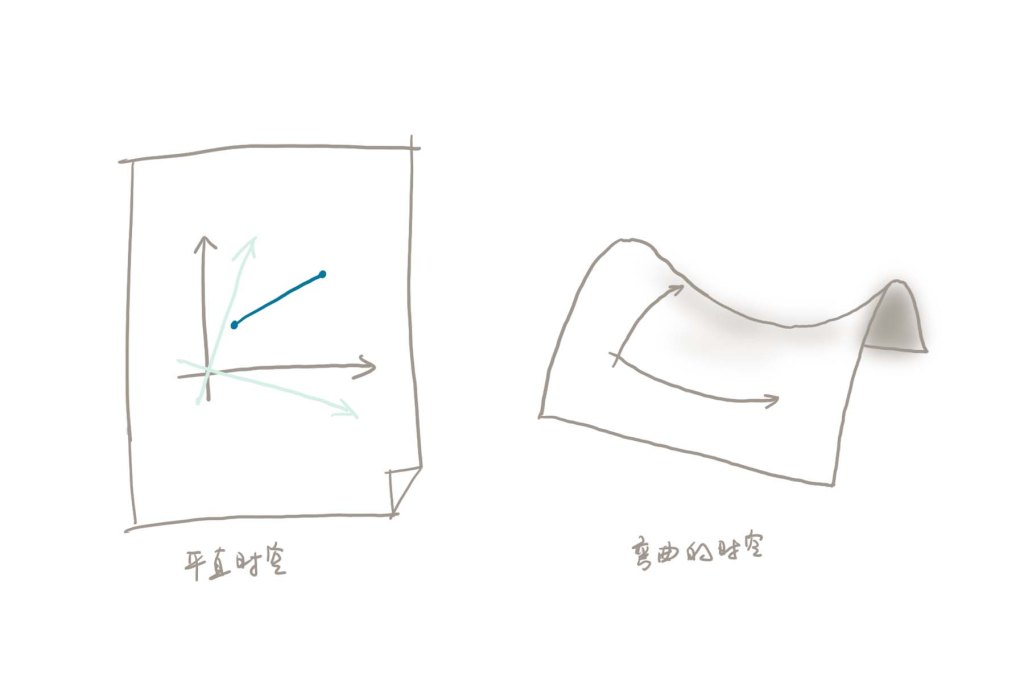
咱们狭义相对论就分享到这里,总之,匀速运动时,时空并没有扭曲。尽管在高速状态下,时间和空间都出现了变化,但这不是扭曲,而是参考系的旋转引发的效应,如下左图。相对的,下方右图才是真正的弯曲空间。要是物体开始加速,故事就来到了广义相对论,时空即开始弯曲,敬请期待!大家的阅读、分享和评论都是我更新的动力源泉,我们下期再见!
【补充】
以上提到的两个参考系之间的旋转变换,就是著名的“洛伦兹变换”。旋转变换是属于“保长变换”,例如我们生活中遇到的空间旋转,就是保证空间间距不变。洛伦兹变换就是属于广义的旋转变换,它控制“固有时”(即时空距离,dt^2 – dx^2)不变,具体形式如下图:
Leave a comment